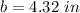Answer:
The minimum width is
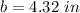
Step-by-step explanation:
The free body diagram is shown on the first uploaded image
The Summation of the moment about A is equal to 0 from the diagram we can see its wedged
i.e
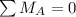
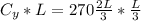
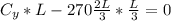
Given from the question that L = 15 ft
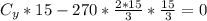
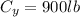
=>
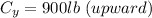
The net upward force experienced by the beam = 0
i.e
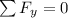 because of the canceling downward force
because of the canceling downward force
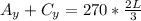
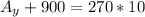

The maximum bending always occurs where the shear force is zero
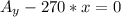
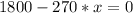
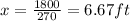
To obtain the maximum bending moment
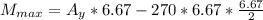
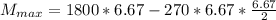
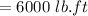
To obtain the width

The equation above is the bending equation
Where M is the bending moment

Note: the multiplication by 12 is to convert the value to inches
I is the moment of inertia
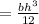
Note: the division by 12 is to convert the value to inches
and
 is the bending stress = 1.95 ×1000 ksi
is the bending stress = 1.95 ×1000 ksi
Then y is the distance from natural axis =
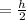
Substituting this into the formula we have
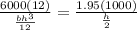
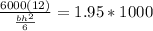
given that
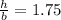
=>h = 1.75 b
Substituting into the equation
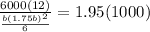
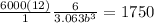
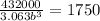
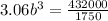

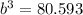
![b = \sqrt[3]{80.593}](https://img.qammunity.org/2021/formulas/physics/college/6ybxlskhryatel9sbu8cr4o2182c18cqvk.png)