Question

Find the parametric equations for the line through the point P(2,4,4) that is perpendicular to the plane −1x+1y−4z=1. a) Use the variable t and write these equations so that t=0 corresponds to the point P.

Answer 1

`(x-2)/(-1) =(y-4)/(1) =(z-4)/(-4) =t`

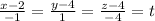
Explanation:

Given that a line passes through P(2,4,4)

Also the line is perpendicular to the plane

`-1x+1y-4z=1.`

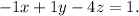
From the equation of the plane we can say that normal to the plane has direction ratios as (-1,1,-4)

Since the required line is also perpendicular to the plane, the direction ratios of the required line is

(-1,1,4)

It passes through (2,4,4)

If Q(x,y,z) are general points on the line then

Direction ratios of PQ are = (x-2, y-4, z-4)

These are proportional to (-1,1,4)

So parametric form of the line is

`(x-2)/(-1) =(y-4)/(1) =(z-4)/(-4) =t`

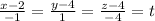
Whem t=0 we get the point P.