Question

In a round robin tennis tournament, each player plays every other player exactly once. Use induction to show that if there are n players there will be n(n − 1)/2 games.

Answer 1

Explanation:

given that in a round robin tennis tournament, each player plays every other player exactly once.

Suppose there are two players i.e. n=2, we have only one match satisfies

`(2(2-1))/(2) =1`

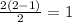
Hence P(2) is true

Assume P(k) is true. For k players no of matches played

=
`(k(k-1))/(2)`

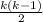
To prove true for n = k+1

If to k players one new player is introduced, then the new player should play all the k players to have the condition satisfied

i.e. no of matches = no for k players + k

=
`(k(k-1))/(2) +k\\= (k^2-k+2k)/(2) \\= ((k+1)k)/(2)`

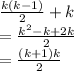
So if true for n =k, then true for n =k+1

Already true for n =2

By induction true for all natural numbers starting from 2.