Answer:
Required probability = 0.066
Explanation:
We are given that Thirty-seven percent of the American population has blood type O+.
Firstly, the binomial probability is given by;
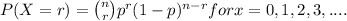
where, n = number of trails(samples) taken = 5 Americans
r = number of successes = at least four
p = probability of success and success in our question is % of
the American population having blood type O+ , i.e. 37%.
Let X = Number of people tested having blood type O+
So, X ~
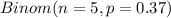
So, probability that at least four of the next five Americans tested will have blood type O+ = P(X >= 4)
P(X >= 4) = P(X = 4) + P(X = 5)
=
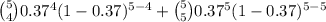
=
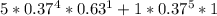 = 0.066.
= 0.066.