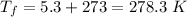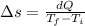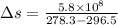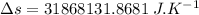Answer:
a)
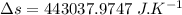
b)
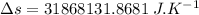
Step-by-step explanation:
a)
Given:
amount of heat transfer occurred,
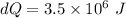
initial temperature of car,
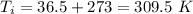
final temperature of car,
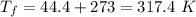
We know that the change in entropy is given by:
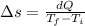
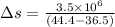 (heat is transferred into the system of car)
(heat is transferred into the system of car)
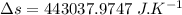
b)
amount of heat transfer form the system of house,
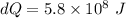
initial temperature of house,
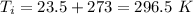
final temperature of house,