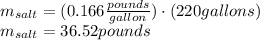Question

A 500-gallon tank initially contains 220 gallons of pure distilled water. Brine containing 5 pounds of salt per gallon flows into the tank at the rate of 5 gallons per minute, and the well stirred mixture flows out of the tank at the rate of 5 gallons per minute. Find the amount of salt in the tank after 8 minutes.

Answer 1

Answer: The amount of salt in the tank after 8 minutes is 36.52 pounds.

Explanation:

Salt in the tank is modelled by the Principle of Mass Conservation, which states:

(Salt mass rate per unit time to the tank) - (Salt mass per unit time from the tank) = (Salt accumulation rate of the tank)

Flow is measured as the product of salt concentration and flow. A well stirred mixture means that salt concentrations within tank and in the output mass flow are the same. Inflow salt concentration remains constant. Hence:

`c_(0) \cdot f_(in) - c(t) \cdot f_(out) = (d(V_(tank)(t) \cdot c(t)))/(dt)`

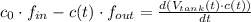
By expanding the previous equation:

`c_(0) \cdot f_(in) - c(t) \cdot f_(out) = V_(tank)(t) \cdot (dc(t))/(dt) + (dV_(tank)(t))/(dt) \cdot c(t)`

The tank capacity and capacity rate of change given in gallons and gallons per minute are, respectivelly:

`V_(tank) = 220\\(dV_(tank)(t))/(dt) = 0`

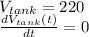
Since there is no accumulation within the tank, expression is simplified to this:

`c_(0) \cdot f_(in) - c(t) \cdot f_(out) = V_(tank)(t) \cdot (dc(t))/(dt)`

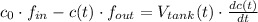
By rearranging the expression, it is noticed the presence of a First-Order Non-Homogeneous Linear Ordinary Differential Equation:

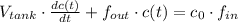`V_(tank) \cdot (dc(t))/(dt) + f_(out) \cdot c(t) = c_0 \cdot f_(in)`, where
`c(0) = 0 (pounds)/(gallon)`.

`(dc(t))/(dt) + (f_(out))/(V_(tank)) \cdot c(t) = (c_0)/(V_(tank)) \cdot f_(in)`

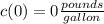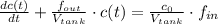
The solution of this equation is:

`c(t) = (c_(0))/(f_(out)) \cdot ({1-e^{-(f_(out))/(V_(tank))\cdot t }})`

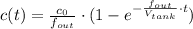
The salt concentration after 8 minutes is:

`c(8) = 0.166 (pounds)/(gallon)`

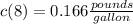
The instantaneous amount of salt in the tank is:

`m_(salt) = (0.166 (pounds)/(gallon)) \cdot (220 gallons)\\m_(salt) = 36.52 pounds`