Answer:
(a).The magnitude and direction of the vector is 4.12 m and 284°
(b). The magnitude and direction of the vector is 19.10 m and 313°
Step-by-step explanation:
Given that,
The three displacement are
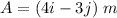

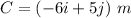
We need to calculate the magnitude of the vector
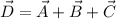
Put the value into the formula
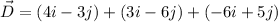

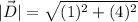

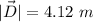
We need to calculate the direction of the vector
Using formula of direction

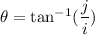
Put the value into the formula
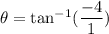
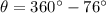
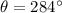
(b). We need to calculate the magnitude of the vector
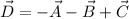
Put the value into the formula
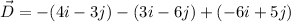
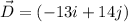

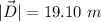
We need to calculate the direction of the vector
Using formula of direction

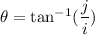
Put the value into the formula
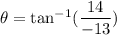
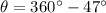
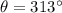
Hence, (a).The magnitude and direction of the vector is 4.12 m and 284°
(b). The magnitude and direction of the vector is 19.10 m and 313°