Question

ndom sample of 16 values is drawn from a mound-shaped and symmetric distribution. The sample mean is 15 and the sample standard deviation is 2. Use a level of significance of 0.05 to conduct a two-tailed test of the claim that the population mean is 14.5

Answer 1

The population mean is not different from 14.5.

Explanation:

The two tailed hypothesis to test whether the population mean is 14.5 or not is:

H₀: The population mean is 14.5, i.e. μ = 14.5.

Hₐ: The population mean is different from 14.5, i.e. μ ≠ 14.5.

The information provided is:

`\bar x=15\\s=2\\\alpha =0.05`

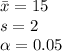
As the population standard deviation is not provided use a t-test for single mean.

The test statistic is:

`t=(\bar x-\mu)/(s/√(n)) =(15-14.5)/(2/√(16))=1`

The test statistic value is 1.

Decision rule:

The critical value of t for α = 0.05 and degrees of freedom, (n - 1) = 15 is:

`t_(0.05/2, 15)=\pm 2.131`

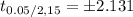
If the test statistic value lies outside the range (-2.131, 2.131) then the null hypothesis will be rejected.

The test statistic value is 1.

This value lies in the range (-2.131, 2.131).

Thus, the null hypothesis was failed to be rejected at 5% level of significance.

Conclusion:

As the null hypothesis was not rejected it can be concluded that the population mean is not different from 14.5.