Answer:
559.5 N at the bottom and 519.6 N at the top of the wheel
Step-by-step explanation:
If it completes 1 revolution (or 2π rad) per 28s then its angular speed is
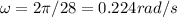
The centripetal acceleration would be:
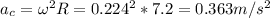
Let gravitational acceleration g = 9.81 m/s2.
At the bottom of the wheel the net acceleration would be g plus the centripetal acceleration:
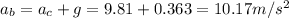
So the weight at the bottom of the wheel would be
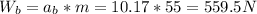
Similarly at the top of the wheel the net acceleration is g subtracted by the centripetal acceleration:
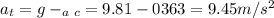
And the weight at the top is
