Question

How to solve this 2 question? ​

Answer 1

8. For brevity, let U = unemployed, E = employed, M = male, F = female. We're given that

P(M) = P(F) = 50/100 = 1/2

P(U) = 60/100 = 3/5

P(M | U) = 2/3

P(E) = 40/100 = 2/5

P(F | E) = 3/4

8a. This follows immediately from the given information. Specifically,

P(E) = 1 - P(U) = 1 - 3/5 = 2/5

8b. By definition of conditional probability,

P(A | B) = P(A and B) / P(B) ⇒ P(A and B) = P(A | B) P(B)

It follows that

P(M and U) = P(M | U) P(U) = 2/3 • 3/5 = 2/5

8c. Using Bayes' rule/the definition of conditional probability,

P(U | F) = P(U and F) / P(F) = P(F | U) P(U) / P(F)

Since F and M are mutually exclusive,

P(F | U) = 1 - P(M | U)

and so

P(U | F) = (1 - 2/3) • 3/5 / [(1 - 2/3) • 3/5 + 3/4 • 2/5] = 2/5

8d. Here we assume gender and employment status are independent, so for instance

P(F and E) = P(F) P(E)

We then have by the inclusion/exclusion principle that

P(F or U) = P(F) + P(U) - P(F and U) = P(F) + P(U) - P(F) P(U)

We also have by the law of total probability

P(F) = P(F and U) + P(F and E)

so

P(F or U) = P(F and U) + P(F and E) + P(U) - P(F) P(U)

By the assumed independence,

P(F or U) = P(F) P(U) + P(F) P(E) + P(U) - P(F) P(U)

P(F or U) = P(F) P(E) + P(U)

P(F or U) = 1/2 • 2/5 + 3/5 = 4/5

9.

a. This is mostly a matter of counting the ways a given type of stamp can fall out.

`P(A) = \frac{\dbinom{20}3}{\dbinom{24}3} = (285)/(506)`

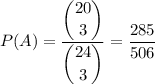
since there are 20 non-green stamps.

`P(B) = \frac{\dbinom21 \dbinom{22}2}{\dbinom{24}3} = (21)/(92)`

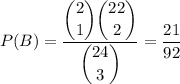
since there are 2 red and unused stamps, 1 of which we want; the other 2 stamps come from the remaining 22 non-red-and-unused stamps.

`P(A \cap B) = \frac{\dbinom21 \dbinom{18}2}{\dbinom{24}3} = (153)/(1012)`

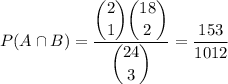
since exactly 1 of the stamps must be red and unused, and the other 2 stamps that fall out can be neither green nor red and unused.

`P(A \cup B) = P(A) + P(B) - P(A \cap B) = (162)/(253)`

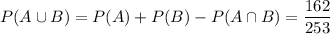
which follows from the inclusion/exclusion principle.

b. There is a total of 10 used stamps, so the probability of at least 1 going missing is

`P(C) = \frac{\dbinom{10}1\dbinom{14}2 + \dbinom{10}2\dbinom{14}1 + \dbinom{10}3}{\dbinom{24}3} = (415)/(506)`

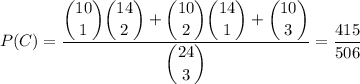
By definition of conditional probability,

`P(C \mid A) = (P(C \cap A))/(P(A))`

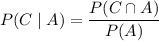
However, there are no used green stamps; any used stamp that goes missing must be red, blue or yellow. So the event A ∩ C is really just the event C, and

`P(C \mid A) = P(C) = (415)/(506)`

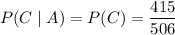
c. A and C are independent if and only if

`P(A \cap C) = P(A) P(C)`

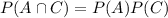
We know

`P(C \cap A) = P(C)`

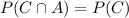
so if A and C are independent, then

`P(C) = P(A) P(C)`

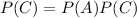
but this would imply P(A) = 1, which is clearly not the case as we found in 9.a. So A and C are not independent.