Question

An open top box is to be built with a rectangular base whose length is twice its width and with a volume of 36 ft 3 . Find the dimensions of the box that minimize the materials used.

Answer 1

The dimensions of the box that minimize the materials used is
`6* 3* 2\ ft`

Explanation:

Given : An open top box is to be built with a rectangular base whose length is twice its width and with a volume of 36 ft³.

To find : The dimensions of the box that minimize the materials used ?

Solution :

An open top box is to be built with a rectangular base whose length is twice its width.

Here, width = w

Length = 2w

Height = h

The volume of the box V=36 ft³

i.e.
`w* 2w* h=36`

`h=(18)/(w^2)`

The equation form when top is open,

`f(w)=2w^2+2wh+2(2w)h`

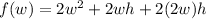
Substitute the value of h,

`f(w)=2w^2+2w((18)/(w^2))+2(2w)((18)/(w^2))`

`f(w)=2w^2+(36)/(w)+(72)/(w)`

`f(w)=2w^2+(108)/(w)`

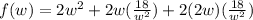
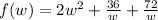
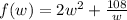
Derivate w.r.t 'w',

`f'(w)=4w-(108)/(w^2)`

For critical point put it to zero,

`4w-(108)/(w^2)=0`

`4w=(108)/(w^2)`

`w^3=27`

`w^3=3^3`

`w=3`

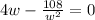
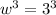
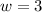
Derivate the function again w.r.t 'w',

`f''(w)=4+(216)/(w^3)`

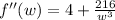
For w=3,
`f''(3)=4+(216)/(3^3)=12 >0`

So, it is minimum at w=3.

Now, the dimensions of the box is

Width = 3 ft.

Length = 2(3)= 6 ft

Height =
`(18)/(3^2)=2\ ft`

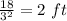
Therefore, the dimensions of the box that minimize the materials used is
`6* 3* 2\ ft`