Question

What is the ratio of the surface areas of two cones if the radius of one is 3 en and the slant height is 7 cm, and the other has a radius of 5 cm and a slan Height of 9 cm?​

Answer 1

Given Information :-

⠀

A cone with dimensions :-

• Radius = 3 cm
• Slant height ( l ) = 7 cm

⠀

Another cone with dimensions :-

⠀

• Radius = 5 cm
• Slant height = 9 cm

⠀

To Find :-

⠀

• The ratio of their total surface area

⠀

Formula Used :-

⠀

`\qquad \diamond \: \underline{ \boxed{ \red{ \sf T.S.A._(Cone)= \pi r(r+l) }}} \: \star`

⠀

Solution :-

⠀

For the first cone,

⠀

Since, we don't really have to find the exact values of the surface area, we will let pi remain as a sign itself, this will make the calculations easier.

⠀

`\sf \longrightarrow T.S.A. = \pi * 3(3 + 7) \\ \\ \\ \sf \longrightarrow T.S.A. = \pi * 3 * 10 \: \: \: \\ \\ \\ \sf \longrightarrow T.S.A. =30 \pi \: {cm}^(2) \: \: \: \: \: \: \: \: \\ \\`

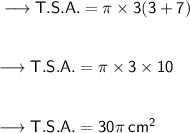
Now, for the second cone,

⠀

`\sf \longrightarrow T.S.A. = \pi * 5(5 + 9) \\ \\ \\ \sf \longrightarrow T.S.A. = \pi * 5 * 14 \: \: \: \: \\ \\ \\ \sf \longrightarrow T.S.A. =70 \pi \: {cm}^(2) \: \: \: \: \: \: \: \: \: \\ \\`

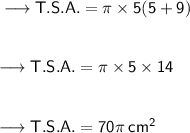
Now, we just have to calculate the ratio of their surface areas, thus,

⠀

`\sf \longrightarrow Ratio = (Surface ~area~of~first~cone)/(Surface ~area~of~second~cone) \\ \\ \\ \sf \longrightarrow Ratio = \frac{30 \pi \: {cm}^(2) }{70 \pi \: {cm}^(2) } \: \: \: \: \: \: \: \: \: \qquad \qquad \qquad \\ \\ \\ \sf \longrightarrow Ratio = \frac{ 3 \cancel{0 \pi \: {cm}^(2)} }{ 7 \cancel{0 \pi \: {cm}^(2) } } \qquad \qquad \qquad \qquad \\ \\ \\\sf \longrightarrow Ratio = (3)/(7) = 3 : 7 \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \\ \\`

Thus, the ratio between the surface areas of the cones is 3 : 7.

⠀

`\underline{ \rule{227pt}{2pt}} \\ \\`