Question

If 90 percent of automobiles in Orange County have both headlights working, what is the probability that in a sample of eight automobiles, at least seven will have both headlights working?

Answer 1

Required probability = 0.8131

Explanation:

We are given that 90 percent of automobiles in Orange County have both headlights working.

Also, a sample of eight automobiles is taken.

Firstly, the binomial probability is given by;

`P(X=r) =\binom{n}{r}p^(r)(1-p)^(n-r) for x = 0,1,2,3,....`

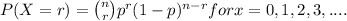
where, n = number of trails(samples) taken = 8

r = number of successes

p = probability of success and success in our question is % of

automobiles in Orange County having both headlights working

i.e. 90%.

Let X = Number of automobiles in Orange County having both headlights working

So, X ~
`Binom(n=8,p=0.9)`

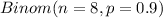
So, probability that in a sample of eight automobiles, at least seven will have both headlights working = P(X >= 7)

P(X >= 7) = P(X = 7) + P(X = 8)

=
`\binom{8}{7}0.9^(7)(1-0.9)^(8-7) + \binom{8}{8}0.9^(8)(1-0.9)^(8-8)`

=
`8*0.9^(7)*0.1 + 1*0.9^(8) *1` = 0.3826 + 0.4305 = 0.8131 .

Answer 2

`P(X \geq 7) = P(X=7) +P(X=8)`

And we can find the individual probabilities using the probability mass function

`P(X=7)=(8C7)(0.9)^7 (1-0.9)^(8-7)=0.3826`

`P(X=8)=(8C8)(0.9)^8 (1-0.9)^(8-8)=0.4305`

And replacing we got:

`P(X \geq 7) = P(X=7) +P(X=8)=0.3826 +0.4305=0.8131`

Explanation:

Previous concepts

The binomial distribution is a "DISCRETE probability distribution that summarizes the probability that a value will take one of two independent values under a given set of parameters. The assumptions for the binomial distribution are that there is only one outcome for each trial, each trial has the same probability of success, and each trial is mutually exclusive, or independent of each other".

Solution to the problem

Let X the random variable of interest "number of automobiles with both headligths working", on this case we now that:

`X \sim Binom(n=8, p=0.9)`

The probability mass function for the Binomial distribution is given as:

`P(X)=(nCx)(p)^x (1-p)^(n-x)`

Where (nCx) means combinatory and it's given by this formula:

`nCx=(n!)/((n-x)! x!)`

And for this case we want to find this probability:

`P(X \geq 7) = P(X=7) +P(X=8)`

And we can find the individual probabilities using the probability mass function

`P(X=7)=(8C7)(0.9)^7 (1-0.9)^(8-7)=0.3826`

`P(X=8)=(8C8)(0.9)^8 (1-0.9)^(8-8)=0.4305`

And replacing we got:

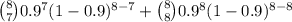
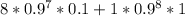`P(X \geq 7) = P(X=7) +P(X=8)=0.3826 +0.4305=0.8131`