Evaluate (1)/(2^(-2)x^(-3)y^(5) ) for x=2 and y=-4. A)-16 b)-4 c)-(1)/(32) d)16

Question

Evaluate
`(1)/(2^(-2)x^(-3)y^(5) )` for x=2 and y=-4.

A)-16
b)-4
c)
`-(1)/(32)`
d)16

Answer 1

`\frac 1{2^(-2)\cdot x^(-3)\cdot y^5}\\\\=\frac 1{2^(-2) \cdot2^(-3) \cdot (-4)^5}\\\\=-\frac 1{2^(-2) \cdot 2^(-3) \cdot (2^2)^5}\\\\=-(1)/(2^(-2) \cdot 2^(-3) \cdot 2^(10))\\\\=-(1)/(2^(-2-3+10))\\\\=-\frac 1{2^(5)}\\\\=-\frac 1{32}`

Answer 2

`\bf C)\: -\cfrac{1}{32}`

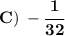
Explanation:

`\tt \cfrac{1}{2^(-2)x^(-3)y^5}`

`\tt x=2\\y=-4`

~

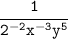
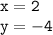
Substitute ''x'' with '2' & 'y' with "-4":-

`\tt \cfrac{1}{2^(-2)* \:2^(-3)\left(-4\right)^5}`

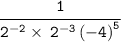
First let's solve
`\tt 2^(-2)* \:\:2^(-3)\left(-4\right)^5`

`\tt 2^(-2)* \:2^(-3)=\boxed{\cfrac{1}{32} }`

`\tt \cfrac{1}{32}\left(-4\right)^5`

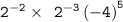
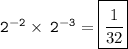
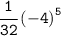
Calculate exponents:- -4^5= -1024

`\tt \cfrac{1}{32}\left(-1024\right)`

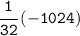
Remove parentheses, apply rule:-
`\tt a\left(-b\right)=-ab`

`\tt-(1)/(32)* \:1024`

`\tt \cfrac{1}{32}* \cfrac{1024}{1}`

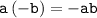
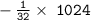
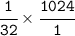
Apply fraction rule:-

`\tt -\cfrac{1* \:1024}{32* \:1}`

`\tt \cfrac{1024}{32}`

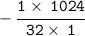
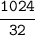
Divide numbers:-

`\tt -32`

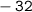
Now that we're done factoring the denominator let's bring down the numerator which is ' 1 ':-

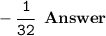
`\tt -\cfrac{1}{32}\;\; \bf Answer`

☆-------☆-------☆-------☆