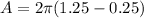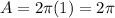Question

Find the area of the surface generated by revolving the curve y= (2x-x^2)^1/2, 0.25<=x<=1.25, about the X-Axis

\(y=\sqrt{2x-x^{2}}\) 0.25 <= x <= 1.25

Answer 1

A = 2π

Explanation:

To calculate the area of the surface generated by revolving the curve

y = √(2x -x²) about the x-axis for the interval 0.25 ≤ x ≤ 1.25 can be found by

`A = 2\pi\int\limits^b_a f(x){√(1+f'(x)) } \, dx`

where f(x) = y = √(2x -x²)

Integrating the f(x) yields

f'(x) = (1 - x)/√(2x -x²)

so the above equation becomes

`A = 2\pi\int\limits^b_a \sqrt{2x - x^(2) } {\sqrt{1+((1-x)/(√(2x-x^2) ) } })^2 \, dx`

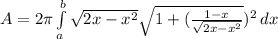
The second term can be simplified to

`{\sqrt{1+((1-x)/(√(2x-x^2) ) } })^2 ={\sqrt{\frac{1}{{2x-x^2} } } }={\frac{1}{{√(2x-x^2)} }`

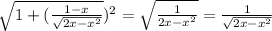
Now equation reduces to

`A = 2\pi\int\limits^b_a \sqrt{2x - x^(2) } (1)/(√(2x-x^2) ) \, dx`

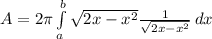
The term √(2x -x²) cancels out

`A = 2\pi\int\limits^b_a \, dx = [x]`

Evaluating the limits

`A = 2\pi(1.25 - 0.25)`

`A = 2\pi(1) = 2\pi`