Question

It is believed that 3% of people actually have this predisposition. The genetic test is 99% accurate if a person actually has the predisposition, meaning that the probability of a positive test result when a person actually has the predisposition is 0.99. The test is 98% accurate if a person does not have the predisposition. What is the probability that a randomly selected person who tests positive for the predisposition by the test actually has the predisposition

Answer 1

Required Probability = 0.605

Explanation:

Let Probability of people actually having predisposition, P(PD) = 0.03

Probability of people not having predisposition, P(PD') = 1 - 0.03 = 0.97

Let PR = event that result are positive

Probability that the test is positive when a person actually has the predisposition, P(PR/PD) = 0.99

Probability that the test is positive when a person actually does not have the predisposition, P(PR/PD') = 1 - 0.98 = 0.02

So, probability that a randomly selected person who tests positive for the predisposition by the test actually has the predisposition = P(PD/PR)

Using Bayes' Theorem to calculate above probability;

P(PD/PR) =
`(P(PD)*P(PR/PD))/(P(PD)*P(PR/PD)+P(PD')*P(PR/PD'))`

=
`(0.03*0.99)/(0.03*0.99+0.97*0.02)` =
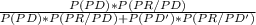
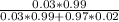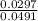`(0.0297)/(0.0491)` = 0.605 .