Answer:
⠀
Explanation :
⠀
For a regular polygon of n sides, we have

⠀
Here, We are to find the measure of each exterior angle of a regular decagon.
⠀
- So, we know a regular decagon has 10 sides, so n = 10 .
⠀
Now, substituting the value :
⠀
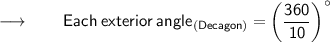
⠀
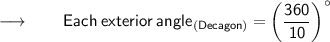
⠀
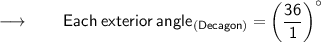
⠀
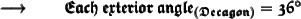
⠀
Therefore,
- The measure of each exterior angle of a regular decagon is 36° .