Question

Each interior angle of a regular polygon has a measure of 40.how many sides does the polygon have?​

Answer 1

Given Information :-

⠀

• Each exterior angle of a regular polygon has a measure of 40°

⠀

To Find :-

⠀

• The number of sides of the polygon

⠀

Formula Used :-

⠀

`\qquad \star \: \underline{ \boxed{ \green{ \sf No.~of~sides = (360^ \circ)/(exterior ~angle)}}} \: \star`

⠀

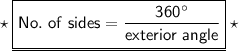
Solution :-

⠀

Using the formula,

⠀

`\sf \dashrightarrow No. ~of~sides= (360)/(40) \\ \\ \\ \sf \dashrightarrow No. ~of~sides= \frac{ \cancel{360}}{ \cancel{40} } \\ \\ \\ \sf \dashrightarrow No. ~of~sides= \underline{ \boxed{ \blue { \frak{9}}}} \: \star`

⠀

Thus, the polygon is a nonagon, and hence has 9 sides.

⠀

`\underline{\rule{227pt}{2pt}} \\ \\`