Answer:
A number line with a point at 3 with a bold line pointing to the right stopping at the open circle at 5.
Explanation:
Phyllis solved the compound inequality
 She began by first breaking the inequality into two separate inequalities
She began by first breaking the inequality into two separate inequalities
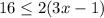 and
and
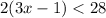 , then she correctly solved each for x:
, then she correctly solved each for x:
1)
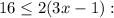
Rewrite this inequality:
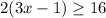
Divide by 2:
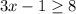
Add 1:
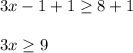
Divide by 3:

2)

Divide by 2:
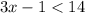
Add 1:
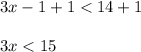
Divide by 3:
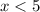
The solution to the compound inequality are all values of x which are greater than 3 or equal to 3 and less than 5. So, you have to plot point at 3, draw a bold line to 5 and plot open circle at 5. Hence, option
A number line with a point at 3 with a bold line pointing to the right stopping at the open circle at 5
is true.