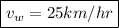Question

A plane flying against the wind covers the 900-kilometer distance between two aerodromes in 2 hours. The same plane flying with the wind covers the same distance in 1 hour and 48 minutes. If the speed of the wind is constant, what is the speed of the wind?

Answer 1

The speed of the wind is 25 km/hr.

Step-by-step explanation:

Let us call
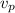`v_p` the speed of the plane and
`v_w` the speed of the wind. When the plane is flying against the wind, it covers the distance of 900-km in 2 hours (120 minutes); therefore;

(1).
`v_p - v_w = (900km)/(120min)`

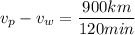
And when the plane is flying with the wind, it covers the same distance in 1 hour 48 minutes (108 minutes)

(2).
`v_p+v_w= (900km)/(108min)`

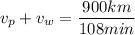
From equation (1) we solve for
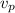`v_p` and get:

`v_p = (900km)/(120min)+v_w`,

and by putting this into equation (2) we get:

`(900km)/(120min)+v_w+v_w= (900km)/(108min)`

`2v_w= (900km)/(108min)-(900km)/(120min)`

`2v_w = 8.3km/min - 7.5km/min`

`2v_w = 0.83km/min`

`v_w = 0.4165km/min`

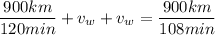
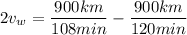
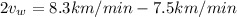
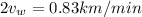
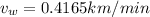
or in km/hr this is

`\boxed{v_w= 25km/hr }`