Question

2. Assume that 12 jurors are selected from a population in which 50% of the people are Mexican-Americans. The random variable x is the number of Mexican-Americans on the jury. x 0 1 2 3 4 5 6 7 8 9 10 11 12 P(x) 0.000 0.003 0.016 0.054 0.121 0.193 0.226 0.193 0.121 0.054 0.016 0.003 0.000 a. Find the probability of exactly 6 Mexican-Americans among 12 jurors. b. Find the probability of 6 or fewer Mexican-Americans among 12 jurors. c. Which probability is relevant for determining whether 6 jurors among 12 is unusually low: the result from part (a) or part (b)? d. Is 6 an unusually low number of Mexican-Americans among 12 jurors

Answer 1

a) 0.226

b) 0.613

c) Part(a)

d) Unusual event

Explanation:

We are given the following in the question:

x: 0 1 2 3 4 5 6 7 8

P(x): 0.000 0.003 0.016 0.054 0.121 0.193 0.226 0.193 0.121

x: 9 10 11 12

P(x): 0.054 0.016 0.003 0.000

a) Probability of exactly 6 Mexican-Americans among 12 jurors.

`P(x = 6) = 0.226`

Thus, 0.226 is the probability of exactly 6 Mexican-Americans among 12 jurors

b) Probability of 6 or fewer Mexican-Americans among 12 jurors

`P(x \leq 6) \\=P(x = 0) + P(x = 1) + P(x =2) + P(x = 3) + P(x = 4) + P(x = 5) + P(x = 6)\\= 0.000+0.003+ 0.016 +0.054 +0.121+ 0.193+ 0.226\\=0.613`

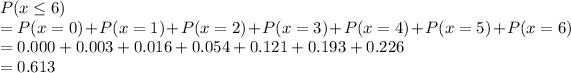
Thus, 0.613 is the probability that 6 or fewer Mexican-Americans among 12 jurors.

c) The result from part​ (a), because it measures the probability of exactly 6

successes.

d) Unusual event

An event is said to be unusual if the probability of event is less than 0.5.

Since

`P(x = 6) = 0.226 < 0.5`

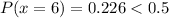
Thus, it is an unusual event as the probability is less than 0.5