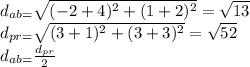Question

Triangle pqr has vertices p(-3 -1) q(-1,-7) and r(3,3) and points a and b are midpoints of segment pq and segment rq respectively.Use coordinate geometry to prove that segment ab is parallel to segment pr and is half the length of segment pr

Answer 1

View graph

Explanation:

Be: p(-3,-1) q(-1,-7) r(3,3)

we must find the value of the middle point a and b

`a=(pq)/(2)\\b=(rq)/(2)`

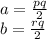
remember that distance between two points is:

`d=\sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2) }`

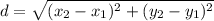
pq=distance between p and q

qr =distance between q and r
`pq=\sqrt{(-1+3)^(2)+(-7+1)^(2)}=\sqrt{(2)^(2)+(-6)^(2)}=√(40)\\ pq=2√(10)\\ a=(pq)/(2)=(2√(10))/(2)=√(10)\\ coordinates\\a=(pq)/(2)=((-3-1,-7-1))/(2)=(-2,-4)\\\\qr=\sqrt{(3+1)^(2)+(3+7)^(2)}=\sqrt{(4)^(2)+(10)^(2)}=√(116)\\qr=2√(29)\\ b=(qr)/(2)=(2√(29))/(2)=√(29)\\ coordinates\\b=(pq)/(2)=((-1+3,-7+3))/(2)=(1,-2)\\`

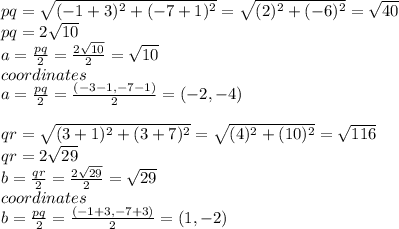
ab is parallel to pr if slope ab is equal to slope pr

`m_(ab)=(-2+4)/(1+2)=(2)/(3)\\m_(pr)=(3+1)/(3+3)=(2)/(3)\\ m_(ab)=m_(pr)`

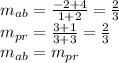
finally distance ab is equal to distance pr/2

`d_(ab=)\sqrt{(-2+4)^(2)+(1+2)^(2)}=√(13)\\ d_(pr=)\sqrt{(3+1)^(2)+(3+3)^(2)}=√(52)\\ d_(ab=)(d_(pr))/(2)`