Question

The lengths of text messages are normally distributed with a population standard deviation of 4 characters and an unknown population mean. If a random sample of 24 text messages is taken and results in a sample mean of 27 characters, find a 99% confidence interval for the population mean. Round your answers to two decimal places. z0.10 z0.05 z0.04 z0.025 z0.01 z0.005 1.282 1.645 1.751 1.960 2.326 2.576 You may use a calculator or the common z-values above.

Answer 1

The 99% confidence interval for population mean μ is (24.90, 29.10).

Explanation:

Let the random variable X is defined as the lengths of text messages.

It is provided that X follows a Normal distribution with an unknown population mean μ and standard deviation σ = 4.

The (1 - α) % confidence interval for population mean is:

`CI=\bar x\pm z_(\alpha /2)* (\sigma)/(√(n))`

Given:

`n=24\\\bar x=27\\z_(\alpha/2)=z_(0.01/2)=z_(0.005)=2.576`

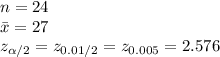
Compute the 99% confidence interval for μ as follows:

`CI=\bar x\pm z_(\alpha /2)* (\sigma)/(√(n))\\=27\pm 2.576*(4)/(√(24)) \\=27\pm 2.1033\\=(24.8967, 29.1033)\\\approx(24.90, 29.10)`

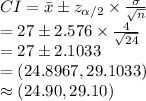
Thus, the 99% confidence interval for population mean μ is (24.90, 29.10).