Question:
On a coordinate plane, a line goes through (negative 3, 2) and (0, 1). A point is at (3, 4). What is the equation of the line that is perpendicular to the given line and passes through the point (3, 4)? y = –One-thirdx + 5 y = –One-thirdx + 3 y = 3x + 2 y = 3x − 5
Answer:
Option D:
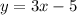 is the equation of the line
is the equation of the line
Step-by-step explanation:
It is given that the line passes through the points
 and
and
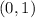
We shall find the equation of the line that passes through the points
 and
and
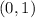
Slope
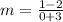
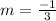
Also, it is given that the line is perpendicular to the line having slope
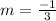
Since, we know that if two lines are perpendicular, then the product of the two slope is equal to -1.
Thus, we have,
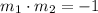
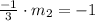
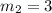
Thus, the slope of the line is
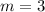 and passes through the point
and passes through the point
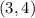
Now, we shall find the equation of the line using the formula,

Thus, we have,

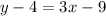
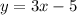
Thus, the equation of the line is
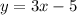
Hence, Option D is the correct answer.