Question

A small particle starts from rest from the origin of an xy-coordinate system and travels in the xy-plane. Its acceleration in the x-direction is 2m/s^2, and its acceleration in the y-direction is 1m/s^2. What is the x-coordinate of the particle when the y-coordinate is 12m?

Answer 1

24m

Step-by-step explanation:

Consider one of the equations of motion as follows;

s = ut +
`(1)/(2)`at² ----------------------------(i)

Where;

s = vertical/horizontal displacement of the body in motion

u = initial vertical/horizontal displacement of the body

t = time taken for the displacement

a = vertical/horizontal acceleration of the body.

Now, since the particle being considered moves in an xy-coordinate system, then equation (i) above can be resolved into the x (horizontal) and y (vertical) components as follows;

Horizontal (x-coordinate) component

`s_(x)` =
`u_(x)` t +
`(1)/(2)`
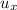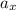`a_(x)`t² ------------------(ii)

Where;

`s_(x)` = horizontal displacement (x-coordinate) of the particle in motion

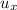`u_(x)` = initial horizontal displacement of the particle

t = time taken for the displacement

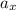`a_(x)` = horizontal (x-direction) acceleration of the body.

Vertical (y-coordinate) component

`s_(y)` =
`u_(y)` t +
`(1)/(2)`
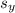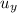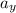`a_(y)`t² -------------------(iii)

Where;

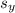`s_(y)` = vertical displacement (y-coordinate) of the particle in motion

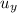`u_(y)` = initial vertical displacement of the particle

t = time taken for the displacement

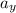`a_(y)` = vertical (y-direction) acceleration of the body.

(A) Now, using equation (iii), from the question;

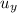`u_(y)` = 0 [since the particle starts from rest, initial velocity is zero]

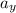`a_(y)` = 1m/s² [acceleration in the y-direction]

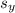`s_(y)` = 12m [y-coordinate value]

Substitute these values into equation (iii) as follows;

12 = 0 t +
`(1)/(2)` (1) t²

12 =
`(1)/(2)` t² [Multiply through by 2]

24 = t² [Solve for t]

t =
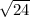`√(24)` seconds

(B) Also, using equation (ii), from the question;

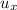`u_(x)` = 0 [since the particle starts from rest, initial velocity is zero]

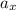`a_(x)` = 2m/s² [acceleration in the x-direction]

`s_(x)` = ? [x-coordinate value]

Substitute these values into equation (ii) as follows;

`s_(x)` = 0 t +
`(1)/(2)` (2) t²

`s_(x)` = t² -------------------(iv)

But t =
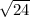`√(24)` seconds as calculated above, substitute this value into equation (iv)

`s_(x)` = (
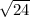`√(24)`)² [Solve for
`s_(x)`]

`s_(x)` = 24

Therefore, the x-coordinate of the particle when the y-coordinate is 12m is 24m

Answer 2

When the y-coordinate is 12m, the x-coordinate of the particle is 24 m

Step-by-step explanation:

Given;

y - component of acceleration = 1 m/s²

X - component of acceleration = 2 m/s²

distance traveled in y - direction, Dy = 12 m

To determine the distance traveled in X- direction, we obtain the duration of the displacement in y- direction.

Applying equation of motion;

Dy = ¹/₂ x at²

`t = \sqrt{(2y)/(a)} = \sqrt{(2*12)/(1)} = 4.9 s`

For distance traveled in x -direction;

Dx = ¹/₂ x at²

Dx = ¹/₂ x 2 x (4.9)² = 24.01 m ≅ 24m

Therefore, when the y-coordinate is 12m, the x-coordinate of the particle is 24 m