Question

The number of defective components produced by a certain process in one day has a Poisson distribution with a mean of 20. Each defective component has probability 0.60 of being repairable.

a) Find the probability that exactly 15 defective components are produced in a particular day. Round your answer to four decimal places.

Answer 1

The probability that exactly 15 defective components are produced in a particular day is 0.0516

Explanation:

Probability function :
`P(X=x)=e^(-\lambda) (\lambda^x)/(x!)`

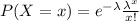
We are given that The number of defective components produced by a certain process in one day has a Poisson distribution with a mean of 20.

So,
`\lambda = 20`

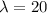
we are supposed to find the probability that exactly 15 defective components are produced in a particular day

So,x = 15

Substitute the values in the formula :

`P(X=15)=e^(-20) (20^(15))/(15!)`

`P(X=15)=e^(-20) (20^(15))/(15!)`

`P(X=15)=0.0516`

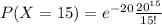
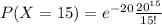
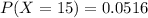
Hence the probability that exactly 15 defective components are produced in a particular day is 0.0516