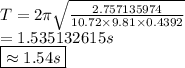
Answer:
1.54 s
Step-by-step explanation:
Considering that the legs constitute 16% of the total weight of the man then mass,

The legs also constitute 48% of his height hence
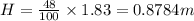
The moment of inertia of a cylinder rotating about a perpendicular axis at one end is
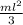 hence
hence
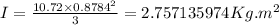
We also know that the period is given by
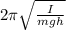
Here, h=0.5H= 0.5*0.8784=0.4392 m
Taking g as 9.81 kg/m2 then