Question

A k out of n system is one in which there is a group of n components, and the system will function if at least k of the components function. Assume the components function independently of one another.

1). In 3 out 5 system, each component has probability 0.9 of functioning. What is the probability that the system will function?
2). Based on the information given in 1), what is the expected number of components that function.
3). In a 3 out n system, in which each component has probability 0.9 of functioning, what is the smallest values of n needed so that the probability that the system functions is at least 0.90?

Answer 1

(a) The probability that the system will function is 0.9914.

(b) The expected number of components that function is 4.5.

(c) The smallest possible value of n is 4 for which the probability of the system function is at least 0.90.

Explanation:

It is provided that a k out of n system will function if at least k components will function out of n.

The distribution of the number of components functioning is Binomial.

Then the probability mass function of the number of components working in a 3 out of 5 system is:

`P(X=x)={5\choose x}p^(x)(1-p)^(5-x)`

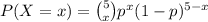
(a)

The probability of a component functioning is, P (X) = p = 0.90.

Now for the system to function at least 3 components must function.

Compute the probability of P (X ≥ 3) as follows:

P (X ≥ 3) = 1 - P (X < 3)

= 1 - P (X = 0) - P (X = 1) - P (X = 2)

`=1-{5\choose 0}(0.90)^(0)(1-0.90)^(5-0)-{5\choose 1}(0.90)^(1)(1-0.90)^(5-1)\\-{5\choose 2}(0.90)^(2)(1-0.90)^(5-2)\\=1-0.00001-0.00045-0.0081\\=0.99144`

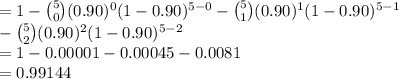
Thus, the probability that the system will function is 0.9914.

(b)

The expected value of a Binomial random variable is:

`E(X)=np`

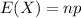
Compute the expected number of components that function as follows:

`E(X)=np=5*0.90=4.5`

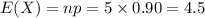
Thus, the expected number of components that function is 4.5.

(c)

• In part (a) we computed the probability of a 3 out of 5 system working as 0.9914.

• Consider a 3 out of 4 system.

Check whether the probability of a 3 out of 4 system functioning is at least 0.90.

Compute the probability of a 3 out of 4 system working as follows:

P (X ≥ 3) = 1 - P (X < 3)

= 1 - P (X = 0) - P (X = 1) - P (X = 2)

`=1-{4\choose 0}(0.90)^(0)(1-0.90)^(4-0)-{4\choose 1}(0.90)^(1)(1-0.90)^(4-1)\\-{4\choose 2}(0.90)^(2)(1-0.90)^(4-2)\\=1-0.0001-0.0036-0.0486\\=0.9477`

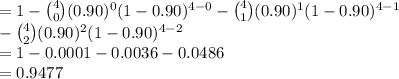
The probability of a 3 out of 4 system working is 0.9477.

• Consider a 3 out of 3 system.

Check whether the probability of a 3 out of 3 system functioning is at least 0.90.

Compute the probability of a 3 out of 3 system working as follows:

P (X ≥ 3) = 1 - P (X < 3)

= 1 - P (X = 0) - P (X = 1) - P (X = 2)

`=1-{3\choose 0}(0.90)^(0)(1-0.90)^(3-0)-{3\choose 1}(0.90)^(1)(1-0.90)^(3-1)\\-{3\choose 2}(0.90)^(2)(1-0.90)^(3-2)\\=1-0.001-0.027-0.243\\=0.729`

The probability of a 3 out of 3 system working is 0.7290.

Thus, the smallest possible value of n is 4 for which the probability of the system function is at least 0.90.