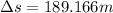Question

A block is sliding on a level surface of varying materials, and so its effective coefficient of friction is variable, 0.1t, where t is the time in seconds for how long the block has been sliding. If the block was initially moving at 43.5 m/s, then how far does it move in 5.1 s

Answer 1

`\Delta s = 189.166 m`

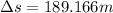
Step-by-step explanation:

The physical for the system is based on Work-Energy Theorem and Principle of Energy Conservation. The system decelerates because of friction before coming to rest:

`K_(1) = W_(loss,1 \longrightarrow 2)`

`(1)/(2) \cdot m \cdot v^(2) = \mu (t) \cdot m \cdot g \cdot \Delta s`

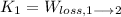
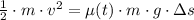
The distance before stopping is isolated from expression presented above:

`\Delta s = ( v^(2))/(2 \cdot \mu(t)\cdot g)`

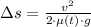
Where
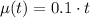`\mu (t) = 0.1\cdot t` and
`g = 9,807 (m)/(s^(2))`.

By replacing all variables, the needed distance is finally found:

`\Delta s = ((43.5 (m)/(s))^(2))/(2 \cdot [0.1\cdot (5.1 sec)]\cdot (9.807 (m)/(s^(2)) ))`

`\Delta s = 189.166 m`