Question

Is the function is even, odd or neither? How do you know?

Answer 1

Explanation:

A function is even if
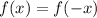`f(x)=f(-x)`, or if the graph has a rotational symmetry about the x-axis. A function is odd if
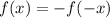`f(x)=-f(-x)`. For example, if you were to reflect that graph about the y-axis. Would it present symmetry?

From the graph we know from the fundamental theorem of Algebra that since f has 3 distinct roots, and changes directions three times, we are dealing with a cubic equation in the form of
`f(x)=x(x+2)(x-2)`

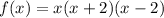
Since the equation is known, try the formulas

First, test for an even function,
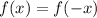`f(x)=f(-x)`, this means that for our function, f,
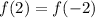`f(2)=f(-2)` see if this holds true

`2(2+2)(2-2) = -2(-2+2)(-2-2)\\2(4)(0)=-2(0)(-4)\\0 = 0`

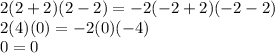
This means that the function is even.