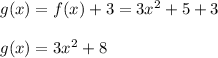Answer:
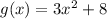
Explanation:
There are some transformations for a function
 . Two of those transformations are:
. Two of those transformations are:
1. If
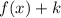 , then the function is translated "k" units up.
, then the function is translated "k" units up.
2. If
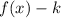 , then the function is translated "k" units down.
, then the function is translated "k" units down.
In this case, you have the following Quadratic function
 given in the exercise:
given in the exercise:
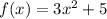
According to the information given, the function
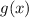 is obtained by translating the Quadratic function
is obtained by translating the Quadratic function
 3 units up. Based on this, you can identify that the transformation is the following:
3 units up. Based on this, you can identify that the transformation is the following:
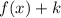
Where
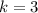
Therefore, you can determine that: