Answer:
0.13J/g°C
Step-by-step explanation:
The mixture of the Iridium in water is in a thermo-equilibrium since no heat is lost to the environment. i.e The heat lost (-
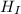 ) by Iridium is equal to the heat gained (
) by Iridium is equal to the heat gained (
 ) by water. This can be represented as follows;
) by water. This can be represented as follows;
-
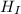 =
=
 --------------------------(i)
--------------------------(i)
The negative sign shows that heat is lost to the environment...
But;
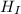 =
=
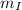
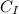 Δ
Δ
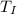 --------------------------(ii)
--------------------------(ii)
Where;
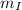 = mass of Iridium
= mass of Iridium
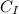 = specific heat capacity of Iridium
= specific heat capacity of Iridium
Δ
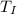 = change in temperature of Iridium =
= change in temperature of Iridium =
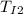 -
-
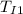
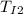 = final temperature of Iridium
= final temperature of Iridium
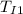 = initial temperature of Iridium
= initial temperature of Iridium
Also;
 =
=
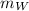
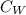 Δ
Δ
 ------------------------(iii)
------------------------(iii)
Where;
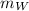 = mass of water
= mass of water
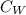 = specific heat capacity of water
= specific heat capacity of water
Δ
 = change in temperature of water =
= change in temperature of water =
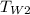 -
-
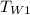
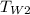 = final temperature of water
= final temperature of water
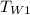 = initial temperature of water
= initial temperature of water
From the question;
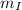 = 23.9g
= 23.9g
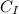 = ?
= ?
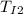 = 22.6°C [the same as the final temperature of water]
= 22.6°C [the same as the final temperature of water]
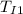 = 89.7°C
= 89.7°C
Δ
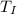 = 22.6°C - 89.7°C = -67.1°C
= 22.6°C - 89.7°C = -67.1°C
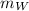 = 20.0g
= 20.0g
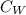 = 4.18 J/g °C
= 4.18 J/g °C
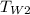 = 22.6°C
= 22.6°C
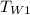 = 20.1°C
= 20.1°C
Δ
 = 22.6°C - 20.1°C = 2.5°C
= 22.6°C - 20.1°C = 2.5°C
Substitute the values of
 and
and
 into equation (i)
into equation (i)
-
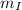
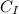 Δ
Δ
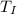 =
=
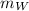
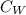 Δ
Δ
 -------------------------------(iv)
-------------------------------(iv)
Now substitute the values of all the variables in equation(iv) into the same;
- 23.9 x
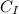 x - 67.1 = 20.0 x 4.18 x 2.5
x - 67.1 = 20.0 x 4.18 x 2.5
1603.69
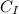 = 209
= 209
Then, solve for
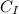 ;
;
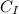 =
=
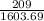
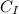 = 0.13
= 0.13
Therefore, the specific heat of Iridium is 0.13J/g°C