Question

HELP ASAPPPP!!!!! this is one of the last few and i don’t know how to do it

Answer 1

Option 3:

elimination using multiplication (3,-1)

Explanation:

The system of equations to be solved are

-5x+3y=-18.......eqn (1)

2x+2y=4. .......eqn (2)

We first multiply eqn(1) by 2 and eqn(2) by 5 to get eqn(3) and eqn(4) respectively.

This implies

-10x+6y=-36.......eqn (3)

10x+10y= 20.......eqn (4)

we then add eqn(3) and eqn(4) to obtain

16y=-16

We divide through by 16

`\implies (16y)/(16)= (16)/(16)`

`\implies y = - 1`

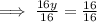
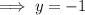
Putting the value of y into eqn(2)

`\implies 2x + 2( -1 ) = 4`

`\implies 2x - 2= 4`

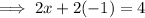
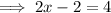
Adding 2to both sides

`\implies 2x - 2+ 2 = 4 + 2`

`\implies 2x= 6`

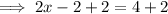
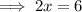
Dividing through by 2

`\implies (2x)/(2) = (6)/(2)`

`\implies x = 3`

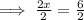
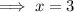
Hence, (x, y)=(3,-1)