Question

(a) The volume V of a growing spherical cell is

V = 4/3pr3,
where the radius is measured in micrometers (1 µm = 10-6m). Find the average rate of change of V with respect to r when r changes from 3 to each of the following. (Round your answers to one decimal place.)
(i) 3 to 6 µm
.......µm3/µm

(ii) 3 to 4 µm
......µm3/µm

(iii) 3 to 3.1 µm
.....µm3/µm

(b) Find the instantaneous rate of change of V with respect to r when r = 3 µm. (Round your answer to one decimal place.)
V'(3) = ......µm3 / µm

Answer 1

(i)=263.9 micrometer square

(ii)=155 micrometer square

(ii)=116.9 micrometer square

(b).37.7 micrometer square

Explanation:

Given,

`f\left ( x \right )=V=4/3\Pi r^(3)`

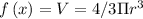
Average rate of change V with respect to a to b where a and b are radius

`\frac{\mathrm{d} V}{\mathrm{d} r} =(f\left ( b \right )-f\left ( a \right ))/\left ( b-a \right )`

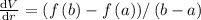
(i) 3 to 6 micrometer

`f\left ( 3 \right )=4/3\Pi * 3^(3)=36\Pi`
`f\left ( 6 \right )=4/3\Pi * 6^(3)=288\Pi`

`\frac{\mathrm{d} V}{\mathrm{d} r}=\left ( f\left ( 6 \right )-f\left ( 3 \right ) \right )/\left ( 6-3 \right )`
`=(288\Pi -36\Pi)/3`

`\frac{\mathrm{d} V}{\mathrm{d} r}=84\Pi =263.893`
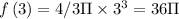
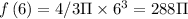
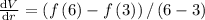
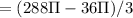
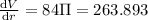
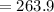`=263.9` micrometer square

(ii) 3 to 4

`f\left ( 4 \right )=4/3\Pi 4^(3)=256\Pi /3`

`\frac{\mathrm{d}V }{\mathrm{d} r}=\left ( f\left ( 4 \right )-f\left ( 3 \right ) \right )/\left ( 4-3 \right )`

`\frac{\mathrm{d} V}{\mathrm{d} r}=(256\Pi /3-36\Pi)/1=154.985`

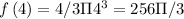
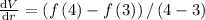
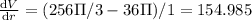
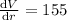`\frac{\mathrm{d} V}{\mathrm{d} r} =155` micrometer square

(iii) 3 to 3.1

`f\left ( 3.1 \right )=4/3\Pi 3.1^(3)=124.788`

`\frac{\mathrm{d} V}{\mathrm{d} r}=\left ( f\left ( 3.1 \right )-f\left ( 3 \right ) \right )/\left ( 3.1-3 \right )`

`=\left ( 124.7882-36\Pi \right )/\left ( 3.1-3 \right )`

`\frac{\mathrm{d} V}{\mathrm{d} r}=116.9091`

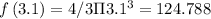
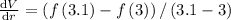
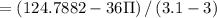
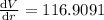
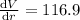`\frac{\mathrm{d} V}{\mathrm{d} r}=116.9` micrometer square

(b) At r=3 micrometer

Instantaneous rate

`\frac{\mathrm{d} V}{\mathrm{d} r}=\frac{\mathrm{d} (4/3\Pi * r^(3))}{\mathrm{d} r}`

`\frac{\mathrm{d} V}{\mathrm{d} r}=4/3\Pi * 3r^(3-1)`

`\frac{\mathrm{d} V}{\mathrm{d} r} =4/3\Pi r^(2)`

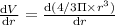
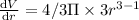
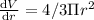
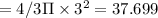`=4/3\Pi * 3^(2)=37.699` micrometer square

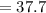`=37.7` micrometer square