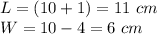Answer:
Part 3)
a)

b)
 and
and

c)
 and
and

d)
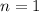 and
and
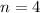
e)
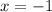 and
and

f)
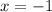 and
and
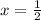
Part 4)
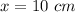
Explanation:
Part 3) Solve the following quadratic equations.
case a) we have

Divide by 4 both sides

take square root both sides

case b) we have
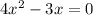
Factor x
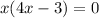
so
One solution is

Second solution is
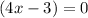

case c) we have

The formula to solve a quadratic equation of the form
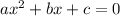
is equal to

in this problem we have

so
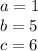
substitute in the formula
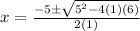
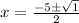
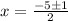
therefore
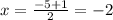
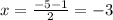
case d) we have
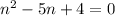
The formula to solve a quadratic equation of the form
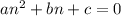
is equal to
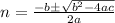
in this problem we have
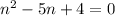
so
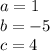
substitute in the formula


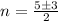
therefore

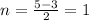
case e) we have
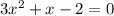
The formula to solve a quadratic equation of the form
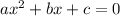
is equal to

in this problem we have
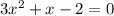
so
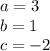
substitute in the formula
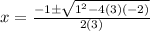
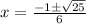
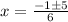
therefore
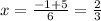
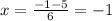
case f) we have
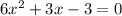
The formula to solve a quadratic equation of the form
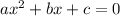
is equal to

in this problem we have
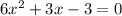
so
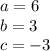
substitute in the formula

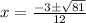
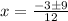
therefore
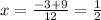
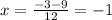
Part 4) we know that
The area of rectangle is equal to
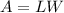
we have

substitute
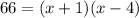
solve for x
Apply distributive property right side

solve the quadratic equation by formula
we have
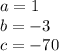
substitute in the formula
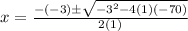
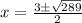
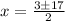
therefore
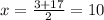
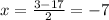 ----> the value of x cannot be negative
----> the value of x cannot be negative
so
The solution is x=10 cm