Answer:
38.22% probability that of 10 randomly selected students, lessthan four will be between 900 and 1,100
Explanation:
For each student, there are only two possible outcomes. Either they score between 900 and 1,100, or they score outside this range. The probability of a student scoring between 900 and 1,100 is independent from other students. So we use the binomial probability distribution to solve this question.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

In which
 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.

And p is the probability of X happening.
About 40 percent of these students’ scores were between 900 and 1,100.
This means that
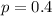 .
.
a)Based on this estimate, what is the probability that of 10 randomly selected students, lessthan four will be between 900 and 1,100?
This is
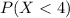 when
when
 . So
. So

In which

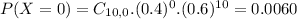
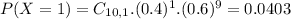
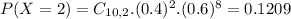
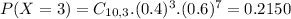
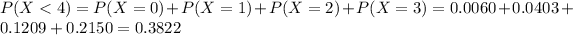
38.22% probability that of 10 randomly selected students, lessthan four will be between 900 and 1,100