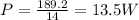Question

A machine carries a 7.0 kg package from an initial position of at t = 0 to a final position of at t = 14.0 s. The constant force applied by the machine on the package is . For that displacement, find (a) the work done on the package by the machine's force and (b) the average power of the machine's force on the package.

Answer 1

a) 189.2 J

b) 13.5 W

Step-by-step explanation:

a)

The work done by the force on the package is equal to the scalar product between force and displacement:

`W=F\cdot d`

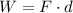
where F is the force and d is the displacement.

In this problem, the force is:

`F=(5.0)i+(6.0)j+(10.0)k[N]`

We know the initial position:

`d_i=(0.6 m)i + (0.75 m)j + (0.28 m)k`

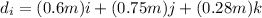
and the final position:

`d_f=(7.5 m)i + (15.0 m)j + (7.2 m)k`

So, the displacement is the difference between the two positions:

`d=d_f-d_i=(7.5-0.6)i+(15.0-0.75)j+(7.2-0.28)k=\\=6.9i+14.25j+6.92k[m]`

Therefore, the scalar product between force and displacement is:

`W=(5.0\cdot 6.9)+(6.0\cdot 14.25)+(10.0\cdot 6.92)=189.2 J`

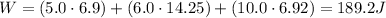
b)

The average power of the machine is the rate of work done per unit time; it is given by

`P=(W)/(t)`

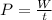
where

W is the work done

t is the time elapsed

In this problem, we have:

W = 189.2 J (work done)

t = 14.0 - 0 = 14.0 s (time elapsed)

Therefore, the average power of the machine is:

`P=(189.2)/(14)=13.5 W`