Question

When an automobile moves with constant velocity, the power developed is used to overcome the frictional forces exerted by the air and the road. If the engine develops 50 hp, what total frictional force acts on the car at 110 mph

Answer 1

`P = F v`

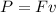
Where: P represent the power in Watts, F the force in Newtons and v the velocity in m/s

`50 hp *(746 W)/(1 hp)= 37300 W`

`110 (mi)/(h) *(1h)/(3600 s) *(1609.34 m)/(1mi)= 49.17 (m)/(s)`

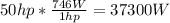
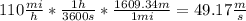
And then we can find the force with the following formula:

`F = (P)/(v)`

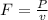
And replacing we got:

`F = (37300 W)/(49.17 m/s)= 758.527 N`

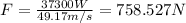
And then the final answer for this case would be 758.52 N acting as the fricitional force.

Step-by-step explanation:

For this case we can use the definition that the power can b expressed in terms of the force and the velocity like this:

`P = F v`

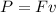
Where: P represent the power in Watts, F the force in Newtons and v the velocity in m/s

We can convert the power into Wtass like this:

`50 hp *(746 W)/(1 hp)= 37300 W`

`110 (mi)/(h) *(1h)/(3600 s) *(1609.34 m)/(1mi)= 49.17 (m)/(s)`

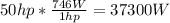
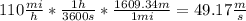
And then we can find the force with the following formula:

`F = (P)/(v)`

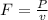
And replacing we got:

`F = (37300 W)/(49.17 m/s)= 758.527 N`

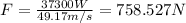
And then the final answer for this case would be 758.52 N acting as the fricitional force.