Solution:
Given Information,
Heat input is (
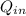 ) = 5.5 ×
) = 5.5 ×
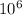 Btu/h
Btu/h
Combustion efficiency of the boiler (
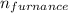 ) = 0.7
) = 0.7
Combustion efficiency after turn up (
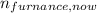 ) = 0.8
) = 0.8
Operation Hour (t) = 5200h
Unit cost (c) =
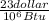
Calculate heat output from the boiler
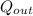 =
=
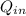 x
x
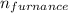
= 5.5 x
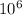 x 0.7
x 0.7
= 3.85 x
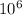 Btu/h
Btu/h
Calculate the heat input to the boiler after the tune-up
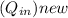 =
=
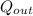 /
/
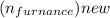
= 3.85 x
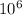 / 0.8
/ 0.8
= 4.8125 x
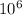 Btu/h
Btu/h
Calculate the saved energy after the tune-up
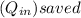 =
=
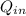 -
-
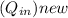
= 5.5 x
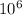 - 4.8125 x
- 4.8125 x
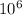 Btu/h
Btu/h
= 0.6875 x
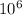 Btu/h
Btu/h
Calculate the annual energy saving (
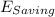 )
)
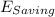 =
=
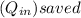 x t
x t
= ( 0.6875 x
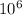 Btu/h ) ( 5200 hr/yr)
Btu/h ) ( 5200 hr/yr)
= 3575 x
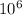 Btu/h
Btu/h
Calculate the annual cost saving
Annual cost saving =
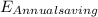 x Unit cost
x Unit cost
= 3575 x
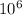 Btu/h x
Btu/h x
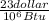
= 82225