Answer:
Present Value (PV) of cash flows are as follows.
(i) Discount rate = 0%
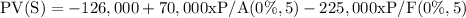
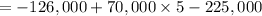
= - 1
Since PV < 0, the project should not be undertaken.
(ii) Discount rate = 2%
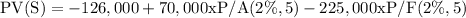
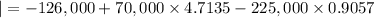
= 156
Since PV > 0, the project should be undertaken.
(iii) Discount rate = 5%
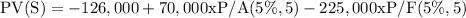
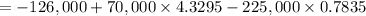
= 772
Since PV > 0, the project should be undertaken.
(ii) Discount rate = 10%
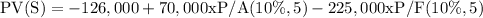
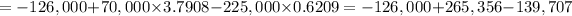
= - 351
Since PV < 0, the project should not be undertaken.