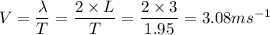Question

Pepe and Alfredo are resting on an offshore raft after a swim. They estimate that 3.0 m separates a trough and an adjacent crest of each surface wave on the lake. They count 11 crests that pass by the raft in 21.5 s. Calculate how fast the waves are moving. (Assume the count begins and ends at the top of a crest.)

Answer 1

The velocity (
`v`) of the wave is 3.08
`ms^(-1)`.

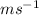Step-by-step explanation:

According to the figure, the distance (
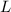`\large{L}`) between a trough and its adjacent crest is
`\large{L = 3 m}`. Also the wavelength (
`\large{\lambda}`) of the wave is
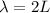`\large{\lambda = 2L}`. Pepe and Alfredo count 11 crests to pass the raft in
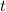`\large{t}` = 21.5 s.

So, the time period (
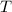`\large{T}`) of oscillation of the wave is

`\large{T} = (t)/(11) = (21.5)/(11) = 1.95s`

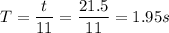
So, the velocity (
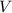`\large{V}`) of the wave is

`\large{V = (\lambda)/(T) = (2 * L)/(T) = (2 * 3)/(1.95)= 3.08 ms^(-1)}`