Question

A 3.49 rad/s (33 1/3 rpm) record has a 4.00 kHz tone cut in the groove. If the groove is located d = 0.080 m from the center of the record (see drawing), what is the wavelength in the groove?

Answer 1

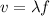`v = \lambda f` (1)

And we have this other relationship between the linear speed and the angular speed:

`v = rw` (2)

We can find the linear velocity like this:

`v = 0.08 m * 3.49 (rad)/(s)= 0.279 m/s`

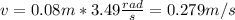
And then from equation (1) we can solve for the frequency and we got:

`\lambda = (v)/(f)`

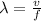
And replacing we got:

`\lambda = (0.279 m/s)/(4000 Hz)= 6.98x10^(-5) m`

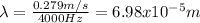
And that represent the wavelength in th groove for this case.

Step-by-step explanation:

For this case we have the following data given:

`w = 3.49 rad/s` represent the angular velocity

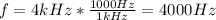`f = 4 kHz *(1000 Hz)/(1 kHz)= 4000 Hz` represent the frequency

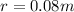`r = 0.08 m` we assume that this respresent the distance from the center

We know the following relationship between the wavelength
`\lambda` and the velocity of a wave:

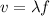`v = \lambda f` (1)

And we have this other relationship between the linear speed and the angular speed:

`v = rw` (2)

We can find the linear velocity like this:

`v = 0.08 m * 3.49 (rad)/(s)= 0.279 m/s`

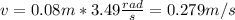
And then from equation (1) we can solve for the frequency and we got:

`\lambda = (v)/(f)`

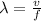
And replacing we got:

`\lambda = (0.279 m/s)/(4000 Hz)= 6.98x10^(-5) m`

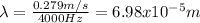
And that represent the wavelength in th groove for this case.