Question

What is the slope of the line?

The graph shows the relationship between the volume of
a rectangular prism and the volume of a square pyramid
with an identical base and height.
Prism vs. Pyramid
+
+
Prism Volume (cubic units)
+
+
1
+
+
2
+
4
+
5
+
+
7
+
8
9
10

Answer 1

correct answer is the 4th option number 3

Answer 2

The slope of the line must be 3

Explanation:

The picture of the question in the attached figure

step 1

we know that

The volume of a rectangular prism is equal to

`V_r_p=Bh` ----> equation A

where

B is the area of the base of the prism

h is the height of the rectangular prism

step 2

The volume of a square pyramid is equal to

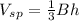`V_s_p=(1)/(3)Bh` -----> equation B

where

B is the area of the square base of pyramid

h is the height of the pyramid

step 3

substitute equation A in equation B

`V_s_p=(1)/(3)V_r_p`

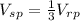
Find the relationship between the volume of a rectangular prism and the volume of a square pyramid

`(V_r_p)/(V_s_p)=3`

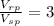
therefore

The slope of the line must be 3

let's check it

To solve for the slope of the line, you must choose two coordinates first and use the formula

`m=(y2-y1)/(x2-x1)`

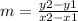
Choosing the points (2,6) and (3,9)

substitute

`m=(9-6)/(3-2)=3` ----> is correct