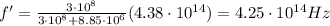Question

Far, far away, a Red Supergiant (wavelength of 685 nm) star suddenly explodes (known as a

supernova). If the supernova was observed on Earth, 5.83x108 lightyears away, how long ago


did the explosion occur? Determine the frequency of the light emitted from the Red Supergiant


before the explosion. Find the observed frequency if the Red Supergiant and the Earth were


moving apart at a speed of 8,850,000 m/s.


Note: 1 year = 365.25 days


c = 3.00 x 108 m/s

Answer 1

1) the explosion occurs
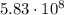`5.83\cdot 10^8` years ago

2)
`4.25\cdot 10^(14) Hz`

Step-by-step explanation:

1)

The light coming from the exploding supernova travels at constant speed, which is the speed of light:

`c=3.0\cdot 10^8 m/s`

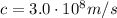
And since it travels with uniform motion, the distance it covers in a time t is given by:

`d=ct`

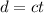
where t is the time taken.

Here, we know that the distance of the supernova from the Earth is

`d=5.83\cdot 10^8 ly`

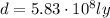
where 1 light-year is the distance covered by light in 1 year. This means that in 1 year, light covers a distance of 1 light-year; in 5 year, light covers a distance of 5 light-years; and so on.

Therefore here, since the distance is

`d=5.83\cdot 10^8 ly`

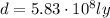
This means that the time taken by light is

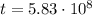`t=5.83\cdot 10^8` years

And therefore, the explosion occurs
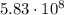`5.83\cdot 10^8` years ago.

2)

First of all, the real frequency of the light emitted by the supernova is given by

`f=(c)/(\lambda)`

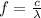
where

c is the speed of light

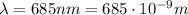`\lambda=685 nm = 685\cdot 10^(-9)m` is the proper wavelength

Substituting,

`f=(3.0\cdot 10^8)/(685\cdot 10^(-9))=4.38\cdot 10^(14) Hz`

The frequency observed on Earth is shifted (Doppler effect) due to the relative motion between the supernova and the Earth; the apparent frequency observed on Earth is given by

`f'=(c)/(c-v)f`

where

c is the speed of light

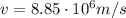`v=8.85\cdot 10^6 m/s` is the speed at which the supernova is moving apart

Substituting the values, we find the apparent frequency:

`f'=(3\cdot 10^8)/(3\cdot 10^8+8.85\cdot 10^6)(4.38\cdot 10^(14))=4.25\cdot 10^(14) Hz`