Question

Pls help me to answer this​

Answer 1

Answers:

Sample Variance = 31.03

Sample Standard Deviation = 5.57

See the table below.

===================================================

Step-by-step explanation:

M refers to the midpoint of each interval. The midpoint is
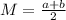`M = (a+b)/(2)` where a,b are the left and right endpoints.

For example,
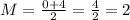`M = (0+4)/(2) = (4)/(2) = 2` in the first row.

Multiply the frequency with the midpoint to get the third column. Summing this column of values leads to 4+49+180+153+154 = 540 shown at the bottom of that column.

Divide this sum over the sum of the frequencies (2+7+15+9+7 = 40) and we arrive at
`\overline{x} = (540)/(40) = 13.5` which is the sample mean xbar.

--------------------------------------------------------------------------

After we determine xbar, we subtract it from each value of M. Then we square the result to get
`(M - \overline{x})^2`. Multiply that with the column f to get the new column
`f(M-\overline{x})^2`.

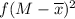This column is added to arrive at 1210 shown in the table below. Divide this over the sum of the frequencies minus 1. So we divide by n-1 = 40-1 = 39 to get roughly 31.03

This is the sample variance.

The square root of this is sqrt(31.03) = 5.57 and this is the approximate sample standard deviation.