The original frequency of horn of Car A is 1071 Hz.
Step-by-step explanation:
Doppler effect describes the change in the frequency of sound waves with respect to the observer. As the sound waves emitted from a source need to travel the air medium to reach observer, it will undergo loss in energy. So there will be change in its frequency compared to original frequency. Depending upon the direction of travel of source and observer the shifting of frequency will vary.
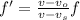
Here vo is the observer velocity and vs is the velocity of the source. So Vo = 15 m/s as car B is the observer and Vs = 35 m/s as car A is the source. And f is the frequency of sound wave at source that is car A.
Similarly, the doppler shift in frequency is the frequency of sound heard by car B which is f' = 1140 Hz. And v is the speed of sound that is v = 343 m/s
1140 =

f = 1140/1.0649= 1071 Hz.
Thus, the original frequency of horn of Car A is 1071 Hz.