Option C:
The scale factor of the larger prism to the smaller prism is
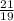 .
.
Solution:
Two rectangular prisms are similar.
Surface area of the smaller prism = 361 cm²
Surface area of the larger prism = 441 cm²
Scale factor of larger prism to smaller prism
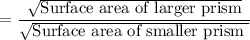
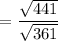
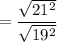
Both square and square roots are cancelled, we get
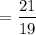
The scale factor of the larger prism to the smaller prism is
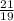 .
.
Hence Option C is the correct answer.