Question

Josiah invests $360 into an account that accrues 3% interest annually. Assuming no deposits or withdrawals are made, which equation represents the amount of money in Josiah’s account, y, after x years?

y = 360(1.3)x
y = 360(0.3)x
y = 360(0.03)x
y = 360(1.03)x

Answer 1

D

Explanation:

Answer 2

y = 360(1.03)x

Explanation:

`F = P x (1 + i)^n`

F is the future worth, P is the present worth, I will be the interest rate, and n is the number of years.
`F = ($360)(1.03)^x`

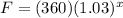
The principal amount of the money = $360

Annual rate of interest = 3%

Thus, the amount after x years which is increased by 3%.

Since, this amount represented by y,

The required equation that represents the amount of money in Josiah’s account, y, after x years is,
`= 360(1+(3)/(100) )^x\\ = 360(1+0.03 )^x\\ = 360(1.03 )^x`

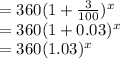
This amount represented by y,

Therefore, the required equation that represents the amount of money in Josiah’s account, y, after x years is,

`y = 360(1.03 )^x`

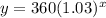
Hope this helps you!

Have a nice evening! ;)