Question

Convert the Cartesian coordinate (6,-3) to polar coordinates, 0≤θ<2π, r>0

Answer 1

The polar coordinates is (3√5 , 333.4°) OR (3√5 , 5.82 rad)

Explanation:

The polar form of the Cartesian coordinates (x , y) is (r , Ф), where

• 
  `r=\sqrt{x^(2)+y^(2)}`
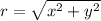
• Ф =
  `tan^(-1)((y)/(x))`

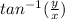
The Cartesian coordinates is (6 , -3)

That means the point lies in the fourth quadrant because the x-coordinate is positive and the y-coordinate is negative, so Ф will be equal [2π -
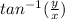`tan^(-1)((y)/(x))` ] (neglect the negative sign of y-coordinate)

∵ x = 6 and y = -3

∵ r > 0

∵
`r=\sqrt{x^(2)+y^(2)}`

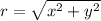
- Substitute x and y in the rule of r

∴
`r=\sqrt{(6)^(2)+(-3)^(2)}`

∴
`r=√(36+9)`

∴
`r=√(45)`

∴
`r=3√(5)`

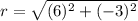
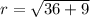
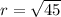
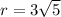
Now let us find Ф

∵ 0 ≤ Ф < 2π

∴ Ф = 2π -
`tan^(-1)((y)/(x))`

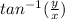
- Neglect the negative sign of the y-coordinate

∴ Ф = 2π -
`tan^(-1)((3)/(6))`

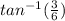
∴ Ф = 333.4° OR Ф = 5.82 radiant

∴ The polar coordinates is (3√5 , 333.4°) OR (3√5 , 5.82 rad)