Answers:
Sample Variance = 31.03
Sample Standard Deviation = 5.57
See the table below.
===================================================
Step-by-step explanation:
M refers to the midpoint of each interval. The midpoint is
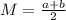 where a,b are the left and right endpoints.
where a,b are the left and right endpoints.
For example,
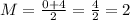 in the first row.
in the first row.
Multiply the frequency with the midpoint to get the third column. Summing this column of values leads to 4+49+180+153+154 = 540 shown at the bottom of that column.
Divide this sum over the sum of the frequencies (2+7+15+9+7 = 40) and we arrive at
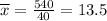 which is the sample mean xbar.
which is the sample mean xbar.
--------------------------------------------------------------------------
After we determine xbar, we subtract it from each value of M. Then we square the result to get
 . Multiply that with the column f to get the new column
. Multiply that with the column f to get the new column
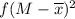 .
.
This column is added to arrive at 1210 shown in the table below. Divide this over the sum of the frequencies minus 1. So we divide by n-1 = 40-1 = 39 to get roughly 31.03
This is the sample variance.
The square root of this is sqrt(31.03) = 5.57 and this is the approximate sample standard deviation.